Mathlas repository

Decision trees provide classifiers that work with a tree-like structure. Given a dataset that you want to classify, you start at the top of the tree and apply the rules you find level by level for each of the points in the dataset. Imagine that you want to classify \(\left(x_1^*, x_2^*\right)=\left(0.3, 0.1\right)\) with the following decision tree:

You'd start at the top, and since \(x_1^* > 0.25\) you'd take the branch on the right, then, since \(x_1^* < 0.7527\) you'd take the branch on the left, and since \(x_2^* < 0.2528\) you'd know that the value assigned by the tree to the point is \(0\).

The main idea behind decision trees (very well explained by Jeremy Kun here; our implementation is based on Jeremy Kun's detailed explanation of the ID3¹ algorithm, although some features of the C4.5² algorithm and some homegrown modifications are present) is that they provide a set of filtering rules that need to be applied in order and that each consecutive filter takes you closer to a conclusion. The concept on which we rely to automatically choose filters which always move towards a conclusion is called the Shannon Entropy³ for a discrete probability \(\left(p_1, \ldots, p_n\right)\), defined as: $$E\left(p_1, \ldots, p_n\right)=-\sum_{i=1}^{n} p_i \log_2\left(p_i\right)$$ This entropy takes values in the range \(\left[0,\log_2\left(n\right)\right]\) and can be seen as how "spread-out" the values of the probability distribution are.
We want to use the training dataset for creating the tree in a way that the probability distribution for the final leaves of the tree (the circles in the chart above) are not spread-out at all; ideally we'd want each final leaf in the tree to provide a 100% probability for a single class (as is the case above).
In order to build a tree, then, we have to explore all the possible values of each splitting variable to determine which one provides a less "spread-out" probability distribution for the splitted data. We construct a metric based on a gain function which compares the entropy of the original dataset with the sum of the entropies of the splitted datasets: $$G\left(S, A\right)=E\left(S\right) - \sum_{v\in V}\frac{\left|S_v\right|}{\left|S\right|}E\left(S_v\right)$$ Where \(S\) is the dataset used for creating the tree (the training dataset), \(A\) is the variable we're using for cutting our dataset, \(v \in V\) are the possible values and \(S_v\) is the subset of \(S\) for which \(A\) takes the value \(v\).

One very important aspect of decision trees built this way is that since the filters are built based on how much "order" they provide, there is no need to perform a variable selection process on the input data; superfluous variables will simply be ignored by the tree construction algorithm.

It would, obviously, make not sense to explore every single value for each variable for real functions (that would just be a map of the values of the function) so we categorise the data by selecting possible threshold points and categorising the data points as being below or above the threshold for the variable in question. We repeat that process for each available real variable (\(x_1\) and \(x_2\) in the example above) and choose the split which results in a higher value for the gain function. For categorical values, we just explore separating the dataset by all the possible values.

We can the perform a simple experiment: try to see how well decision trees "learn" the patterns behind several mathematical functions that take values for \(x_1 \in \left[0, 1\right]\), \(x_2 \in \left[0, 1\right]\). The plot below shows how well our decision tree implementation understands a box function. The plot on the left shows the actual classes for the points whereas the right side shows the values as predicted by a decision tree trained on a similar (but not equal) dataset:

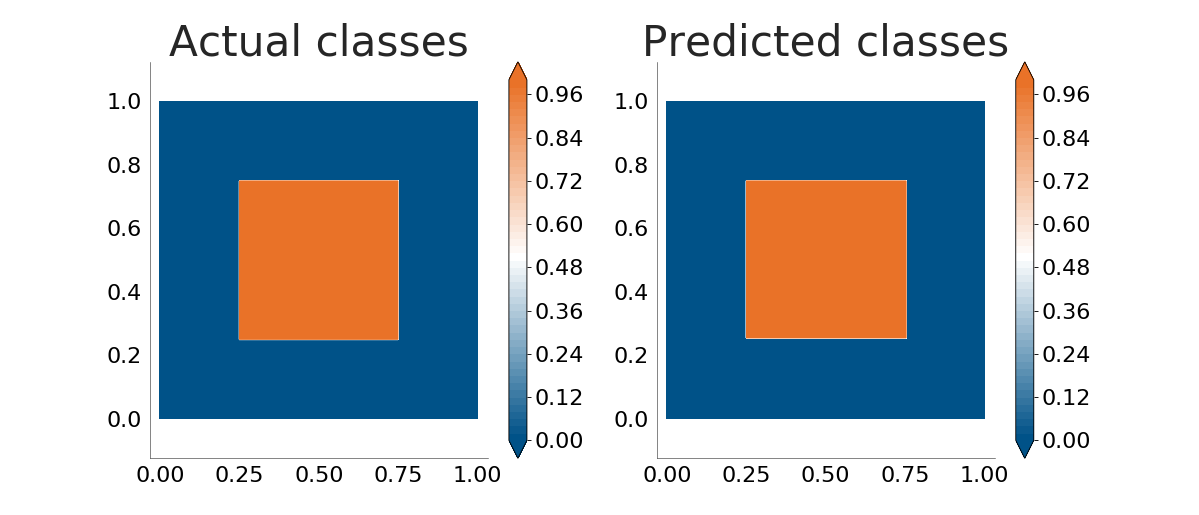
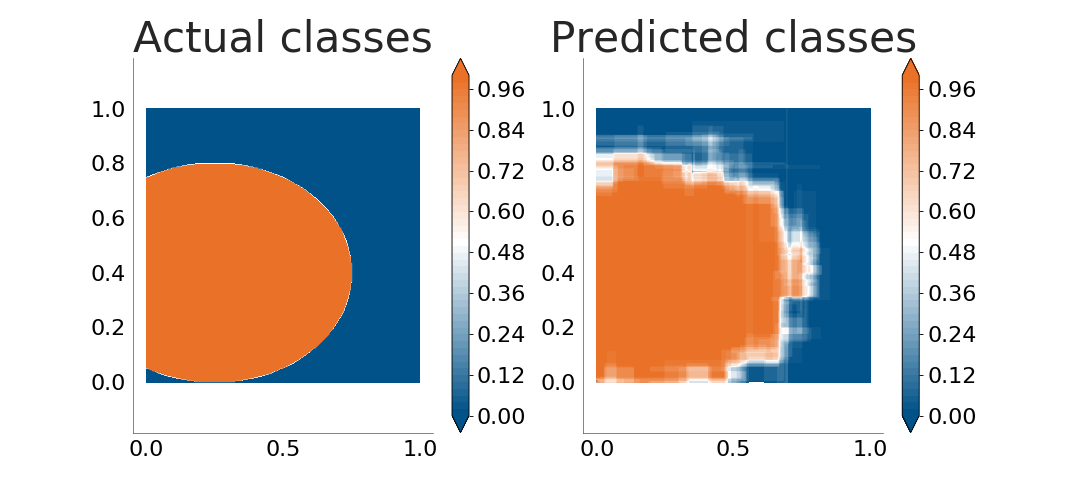
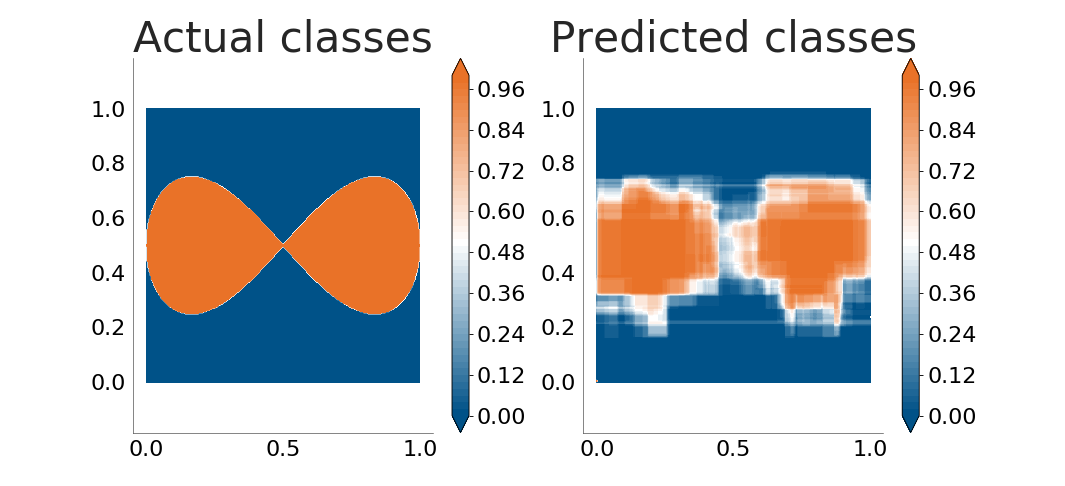
The decision tree does a very good job. Let's see how well it handles boundaries between classes which are not parallel to the coordinate axes. The following plots show how well the decision tree learns an ellipse and a lemniscate:

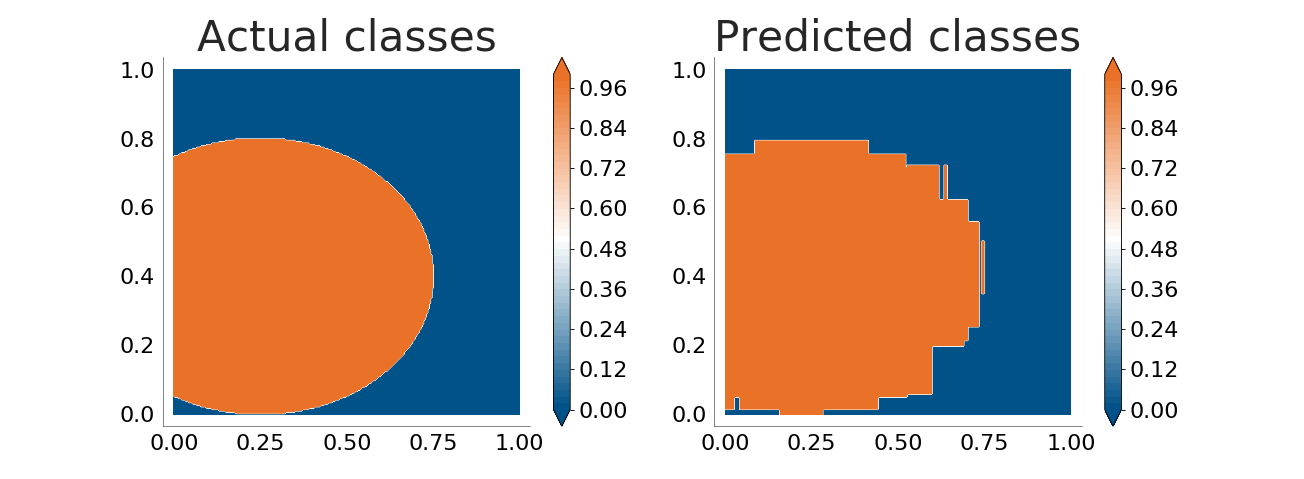
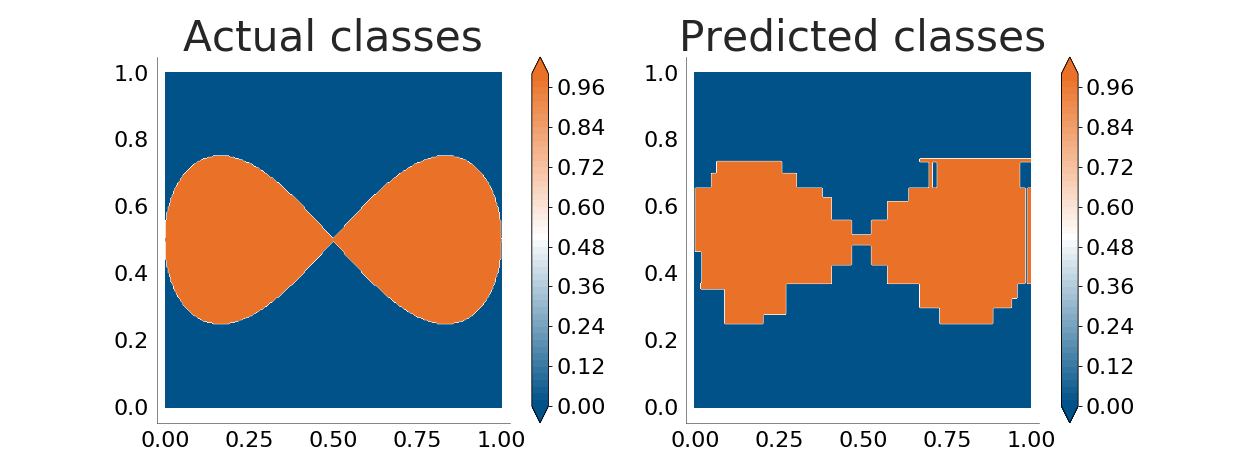
It is now obvious that the decision tree is not good enough when the boundaries between classes are not parallel to the coordinate axes. The problem grows when there's noise in the input data (because of errors in the data sampling process or because the process being monitored does not follow a clear, straight separation between classes):

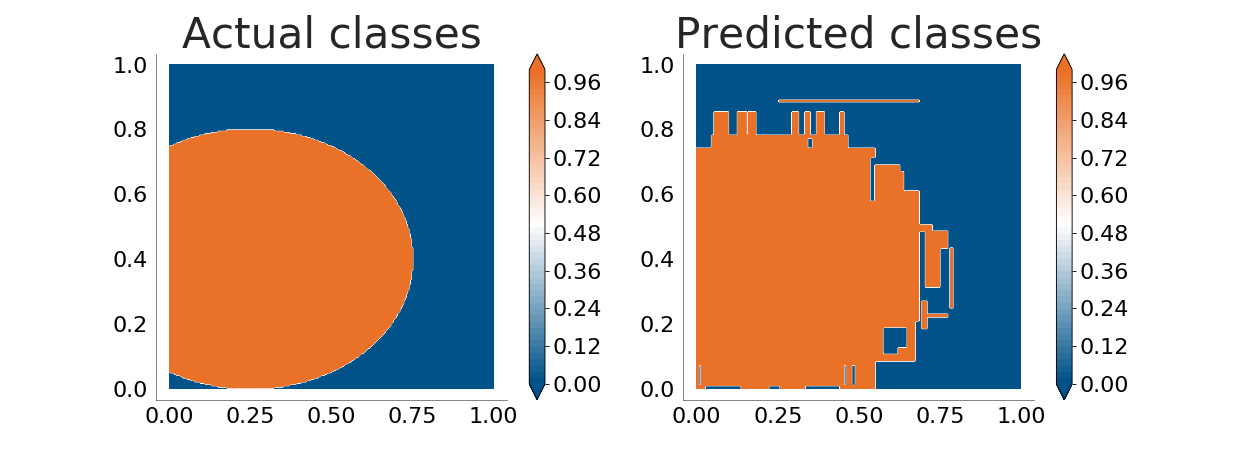
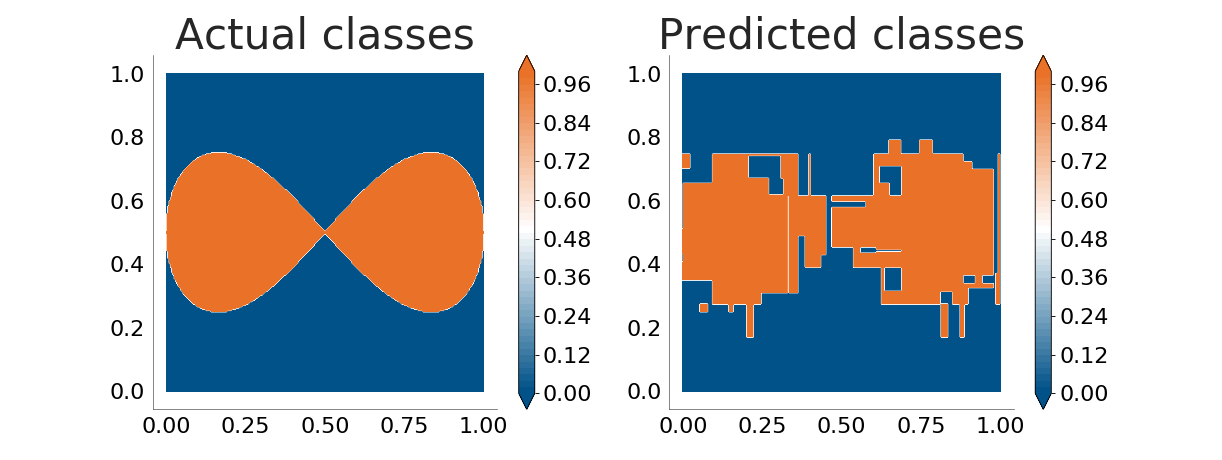
With a 4% level of noise in the training data, overfitting is added to the problem decision trees have with boundaries.

Random forests are classifiers constructed by creating a decision pool based on multiple decision trees. They do not provide absolute classifications, they instead provide probabilities that the given evaluation point falls in each of the possible categories.

The input dataset \(S\) is first divided into a training subset \(S_t\) and an evaluation subset \(S_e\).
\(n_{trees}\) are then trained, each using \(n_{samples}\) random samples and \(n_{tree\_vars}\) random features from \(S_t\) as their training data.

The prediction of the random forest is computed as the weight-average of the precisions of each decision tree. These weights \(w_i\) are defined as the precision of each of the trees when categorising the data in \(S_e\).

We can perform the same exercise as before:

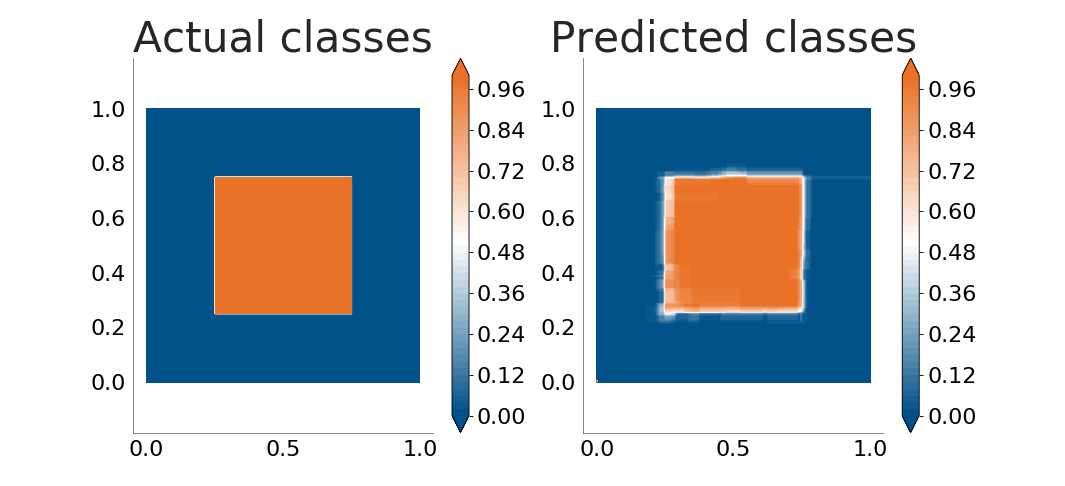
The random forest (constructed with a low value of \(n_{samples}\)) does a poorer job than directly using a decision tree with the centered square. It does, however, add a very important capability: the random forest model provides a level of certainty; it knows where it is less certain about its own capabilities.

Let's do the same exercise with the ellipse and the lemniscate again:

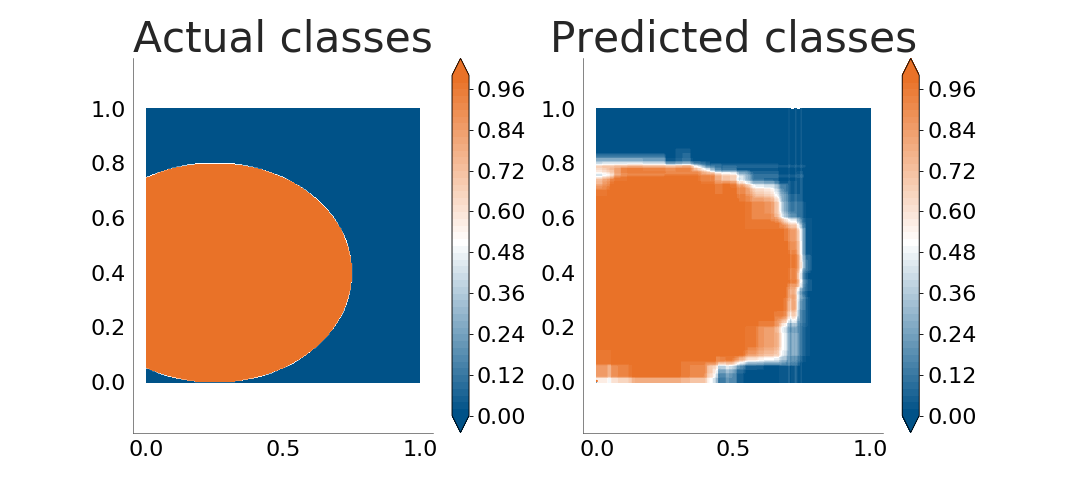
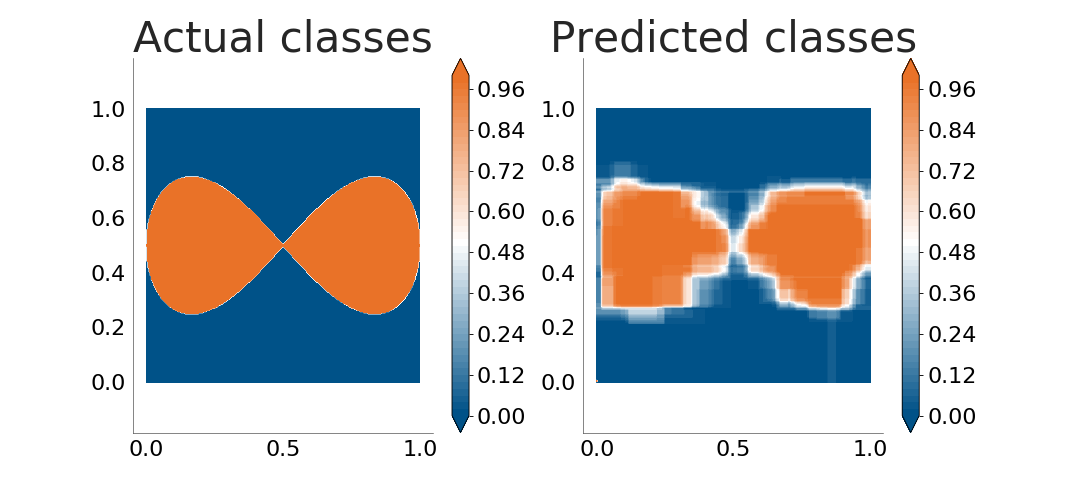
We can perform the example again with a 4% level of noise in the training dataset:

Random forests produce less overfitted results than decision trees.

The AdaBoost algorithm⁴ creates a classifier by constructing a decision pool of learners each of which classify data slightly better than random guessing (weak learners). Our implementation provides a binary AdaBoost classifier that uses decision trees as weak learners.

In the random forest algorithm we trained a set of learners by randomly selecting their training data (based on some user-provided criteria) and evaluated them against \(S_e\). Those learners that performed better were given more weight when evaluating the pool's final decision. In AdaBoost we do something different: we also train a set of learners, but we improve (boost) them a number of rounds by intelligently selecting their training data.

The main idea behind AdaBoost is that, once we've trained our first weak learner, we evaluate it to see which samples are classified worst and make sure that those samples have a higher probability of being presented to the learner as input data on the next boosting round.
This way the learner is presented with samples which were difficult to learn on previous rounds and we make sure that at each round it works on improving its ability to classify those and not "easy" points.

One main advantage of AdaBoost is that it prevents overfitting.

• ¹ Quinlan, J. R. Induction of Decision Trees. Mach. Learn. 1, 81–106 (1986).
• ² Quinlan, J. R. C4.5: Programs for Machine Learning. Morgan Kaufmann San Mateo California 1, (1992).
• ³ Shannon, C. A Mathematical Theory of Communication. System 27, 379–423 (1948).
• ⁴ Schapire, R. E. & Singer, Y. Improved boosting algorithms using confidence-rated predictions. Mach. Learn. 37, 297–336 (1999).